Sommaire
Retour Matlab
Dans tous les exemples précédents, la mise en forme des graphiques n’est pas complète. Afin de produire des graphiques pertinents, il est indispensable d’ajouter un titre (title) des légendes (legend), de préciser les grandeurs et leurs unités sur chacun des axes (xlabel, ylabel)… Vous pouvez vous inspirer du tutoriel MATLAB / Signaux et affichages.
Définir un système
Un système peut-être mathématiquement modélisé par sa fonction de transfert \(H(p)\), qui est une fraction rationnelle de deux polynomes \(N(p)\) et \(D(p)\). Il s’agit de la relation qui lie le signal d’entrée au signal de sortie en fonction de la fréquence du signal d’entrée.
Ces polynômes peuvent se mettre sous la forme suivante : \(N(p) = a_n \cdot p^n + … + a_1 \cdot p^1 + a_0\) et \(D(p) = b_m \cdot p^m + … + b_1 \cdot p^1 + b_0\)
Sous Matlab, il faut stocker ces coefficients sous forme d’un vecteur, allant du poids le plus fort (n ou m) jusqu’au poids le plus faible.
num = [an ... ai ... a0]; den = [bm ... bi ... b0];
Dans l’exemple suivant, on déclare les polynômes suivants : \(A2num(p) = p^1 + 40\) et \(A2den(p) =p^2 + p^1 + 1\)
A2num = [1 40]; % numérateur d'une fonction de transfert - ordre 1 (du poids fort (=- s1 - au poids faible - s0) A2den = [1 1 1]; % dénominateur d'une fonction de transfert - ordre 2
Il est alors possible de créer un système par la fonction tf. Cette fonction nécessite 2 paramètres qui sont les coefficients du numérateur et les coefficients du dénominateur, mis en forme comme vu précédemment.
A2 = tf(A2num, A2den);
Ainsi A2 est un système défini par la fonction de transfert suivante : \(A2(p) = \frac{p^1 + 40}{p^2 + p^1 + 1}\).
Une fois que le système est défini, il est alors possible d’obtenir les réponses indicielle, impulsionnelle ou fréquentielle de ce dernier.
Afficher la réponse indicielle
Pour afficher la réponse indicielle d’un système, il faut utiliser la fonction step.
step(A)
Dans le cas précédent, l’outil de calcul de Matlab adapte les échelles de temps et produit un graphique “pertinent” vis-à-vis des constantes de temps mises en jeu dans le système.
Il est également possible de spécifier le vecteur temps sur lequel on souhaite réaliser la simulation par le programme suivant :
Ttot = 1 t = linspace(0, Ttot, 1001); [IND_A, Time_A] = step(A, t);
Cette méthode s’avérera utile lorsqu’on voudra comparer les réponses indicielles de différents systèmes sur une même graphique (voir aussi tutoriel Matlab / Signaux et affichage).
On peut alors afficher le vecteur IND_A (contenant les valeurs de la réponse indicielle) en fonction du vecteur Time_A (contenant les valeurs de instants considérés) dans une figure.
figure() plot(Time_A, IND_A); grid on;
Afficher la réponse impulsionnelle
Pour afficher la réponse impulsionnelle d’un système, il faut utiliser la fonction impulse.
impulse(A)
Dans le cas précédent, l’outil de calcul de Matlab adapte les échelles de temps et produit un graphique “pertinent” vis-à-vis des constantes de temps mises en jeu dans le système.
Il est également possible de spécifier le vecteur temps sur lequel on souhaite réaliser la simulation par le programme suivant :
Ttot = 1 t = linspace(0, Ttot, 1001); [IMP_A, Time_A] = impulse(A, t);
Cette méthode s’avérera utile lorsqu’on voudra comparer les réponses impulsionnelles de différents systèmes sur une même graphique (voir aussi tutoriel Matlab / Signaux et affichage).
On peut alors afficher le vecteur IMP_A (contenant les valeurs de la résponse impulsionnelle) en fonction du vecteur Time_A (contenant les valeurs de instants considérés) dans une figure.
figure(1) plot(Time_A, IMP_A); grid on;
Afficher la réponse fréquentielle
Pour afficher la réponse fréquentielle d’un système, il faut utiliser la fonction bode.
bode(A)
Dans le cas précédent, l’outil de calcul de Matlab adapte les échelles de temps et produit un graphique “pertinent” vis-à-vis des constantes de temps mises en jeu dans le système.
Il est également possible de spécifier le vecteur de pulsations (fréquences à un facteur \(2\pi\)) sur lequel on souhaite réaliser la simulation par le programme suivant :
w = logspace(0, 5, 101); [mag_A, phase_A, w_A] = bode(A, w); mag_A = squeeze(mag_A); phase_A = squeeze(phase_A); w_A = squeeze(w_A);
La fonction bode est capable de traiter des systèmes multi-entrées et multi-sorties. Les objets de sortie de cette fonction sont alors des tableaux de vecteurs. La fonction squeeze permet dans le cas d’un système à une entrée et une sortie de limiter au seult vecteur disponible (en module et en phase).
On peut alors afficher, dans deux sous-figures différentes (utilisation de subplot), le vecteur mag_A (contenant les valeurs du module de la réponse fréquentielle) en fonction du vecteur w_A (contenant les valeurs de pulsations considérées) et le vecteur phase_A (contenant les valeurs de la phase de la réponse fréquentielle).
figure() subplot(2,1,1) semilogx(w_A, 20*log10(abs(mag_A))); grid on; subplot(2,1,2) semilogx(w_A, phase_A); grid on;
Mettre en cascade (série) deux systèmes
Il est possible de mettre deux systèmes en série par la fonction series.
A1 = 2; % Amplification simple A = series(A1, A2);
Contre-réaction
On peut définir une nouvelle fonction de transfert \(B(p)\) correspondant à la boucle de retour :
Bnum = [1]; % numérateur - ordre 0 Bden = [1 10]; % dénominateur - ordre 1 B = tf(Bnum, Bden);
Pour pouvoir réaliser un système bouclé ayant une réaction A et une contre-reaction B, il suffit d’utiliser la fonction feedback.
TFboucle = feedback(A, B);
Cette fonction permet alors de simuler le système schématisé de la façon suivante :
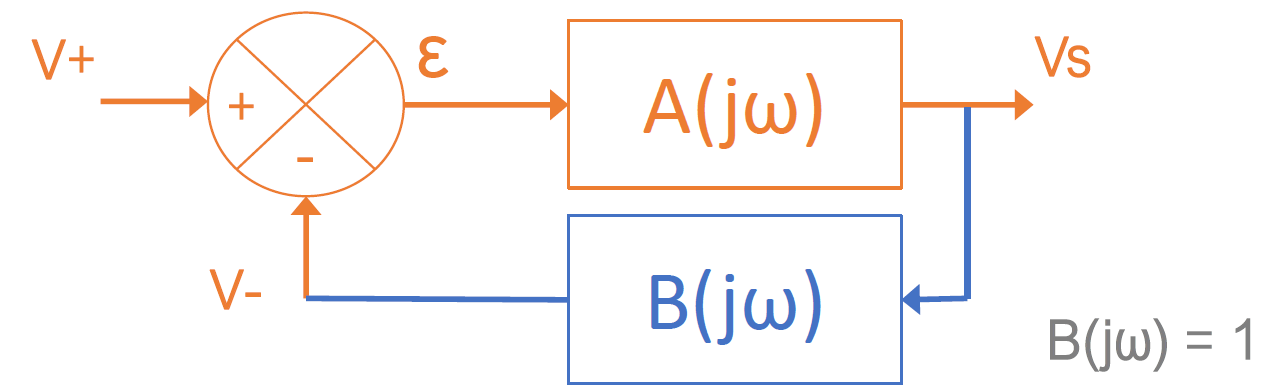
On peut alors afficher les réponses indicielles des deux systèmes :
[TF_boucle, Time_boucle] = step(A);
fonction lsim pour la réponse à un signal particulier
Calculer les marges de sécurité d’un système
Lorsqu’on reboucle un système pour l’asservir, il est indispensable de vérifier que son comportement ne deviendra pas instable. Pour cela, il existe des conditions particulières qu’il faut vérifier en boucle ouverte. On appelle ces limites les marges de gain et de phase.
On appelle marge de phase l’écart entre la valeur -180° et la phase du point de pulsation \(\omega_{0dB}\) (pulsation pour un gain de 0dB).
On appelle marge de gain l’écart entre le gain du point de pulsation \(\omega_{-180}\) (pulsation pour une phase de -180°) et la valeur 0dB.
Le système sera stable en boucle fermée si :
- la marge de phase est positive, c’est à dire si la phase pour un gain de 0dB est supérieure à -180° ;
- la marge de gain est positive, c’est à dire que le gain correspondant à une phase de -180° est strictement négatif.
Ces marges de sécurité peuvent être trouvées de deux façons différentes.
Méthode graphique
Il est possible d’afficher le diagramme de Bode (ou réponse en fréquence) d’un système directement avec la fonction bode de Matlab.
bode(H)
Dans la fenêtre graphique qui s’ouvre, où s’affiche le diagramme de Bode, il est possible d’ajouter les marges de stabilité en faisant un clic-droit sur la zone graphique puis de sélectionner Characteristics / All Stability Margins.
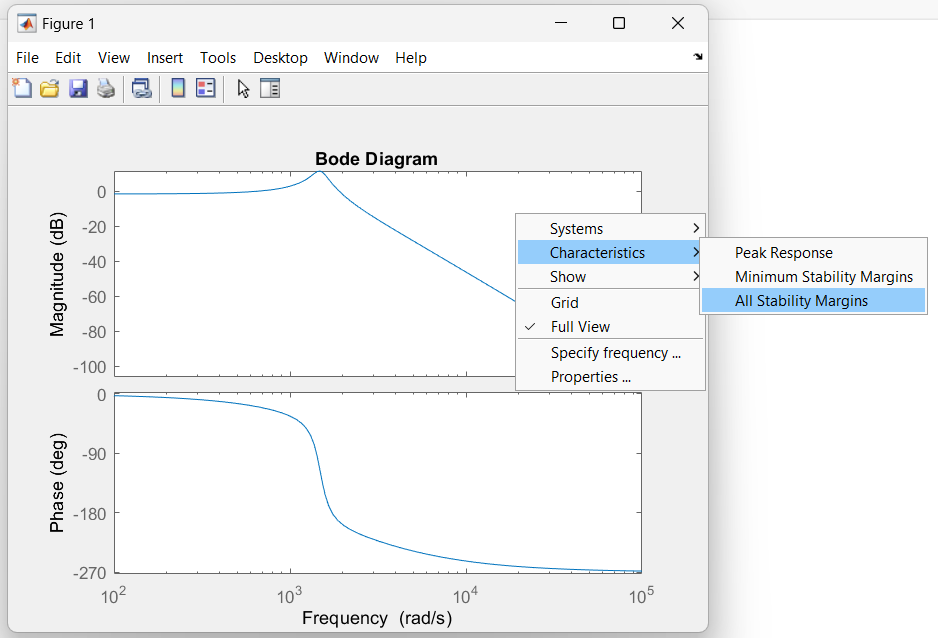
Des points apparaissent alors sur le graphique correspondant à la marge de gain et à la marge de phase. En cliquant dessus, on obtient les informations concernant les marges du système et la stabilité du système bouclé.
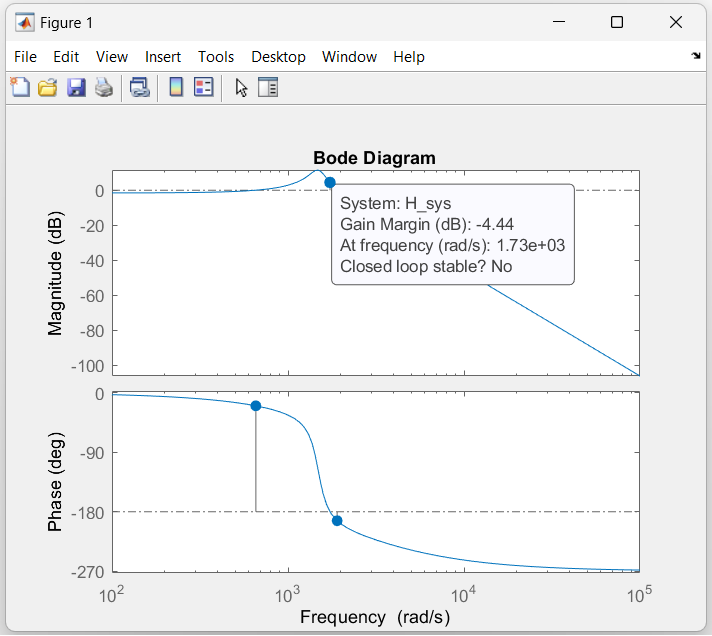
Fonction margin
Matlab propose la fonction margin qui nécessite un système en paramètre et qui renvoie la marge de gain (Gm) et la marge de phase (Pm) de ce système.
[Gm,Pm] = margin(H)
Lorsque le système est instable en boucle fermée (lorsqu’il sera asservi) Matlab renvoie même un message dans la console :


