Retour Matlab
Page en construction !!
Calculer la FFT d’un signal
Un des calculs les plus utilisés dans le traitement du signal (électrique ou traitement d’image) est la transformée de Fourier discrète. L’un des algorithmes permettant d’obtenir ce résultat est la FFT (Fast Fourier Transform). Matlab permet de calculer le spectre d’un signal en utilisant la fonction fft.
Cette fonction retourne un vecteur de nombres complexes de la même taille que le vecteur du signal d’entrée dont on veut connaitre la transformée de Fourier. Les fréquences associées sont comprises entre 0 et Fe – où Fe est la fréquence d’échantillonnage utilisée pour acquérir (ou créer) le signal d’entrée.
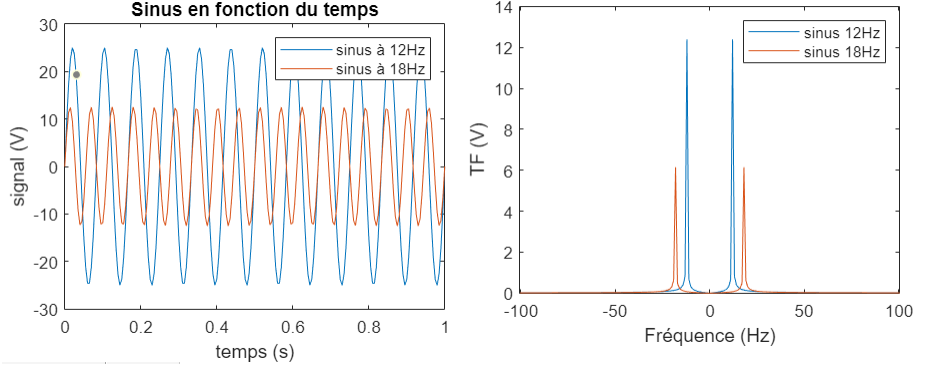
Le script suivant génère deux signaux sinusoïdaux de N échantillons chacun sur une durée de visualisation TA (en s). Le premier a une fréquence f1 et l’autre f2. fa et fb sont les deux signaux numériques. La figure 1 affiche les deux signaux échantillonnées et la figure 2 les transformées de Fourier de deux signaux.
%% Time signals / discrete time
f1 = 12;
f2 = 18;
amp = 25;
N = 201;
TA = 1;
Fe = (N-1)/(TA); % sampling frequency
ta = linspace(0,TA,N);
tb = [0:TA/(N-1):TA];
fa = amp * sin(2*pi*f1*ta);
fb = amp/2 * sin(2*pi*f2*ta);
figure(1);
plot(ta, fa, ta, fb);
legend('sinus à 12Hz','sinus à 18Hz')
xlabel('temps (s)')
ylabel('signal (V)')
title('Sinus en fonction du temps')
%% FFT calculation and display
freqa = linspace(-Fe/2,Fe/2,N);
tfa = fft(fa);
tfa_s = fftshift(tfa)/N;
tfb = fft(fb);
tfb_s = fftshift(tfb)/N;
figure(2);
plot(freqa,abs(tfa_s),freqa,abs(tfb_s));
xlabel('Fréquence (Hz)')
ylabel('TF (V)')
legend('sinus 12Hz','sinus 18Hz')
Le script précédent permet d’obtenir les deux figures suivantes :