Sommaire
Numpy est une bibliothèque incontournable pour les scientifiques.

Les deux principales motivations de son utilisation sont :
- l’implémentation de la notion de vecteur et de matrice dans Python
- l’accès aux fonctions mathématiques classiques (fonctions trigonométriques par exemple)
Cette bibliothèque permet la mise en forme des données pour de nombreuses autres bibliothèques scientifiques plus poussées : Pandas, Scipy, Scikit-image, OpenCV, Kears, Tensorflow…
Pour plus d’information sur cette bibliothèque : https://numpy.org/
Installation de la bibliothèque
Numpy est installée par défaut avec la plupart des distributions Python (comme Anaconda). Elle peut cependant être installé sur Python par l’une des commandes suivantes (dépendant de votre distribution) :
pip install numpy conda install numpy
Importation de la bibliothèque
Afin de pouvoir utiliser la bibliothèque Numpy dans vos scripts sous Python, il est indispensable de l’importer dans votre programme :
import numpy as np
Fonctions mathématiques
Numpy est avant tout une bibliothèque consacrée aux mathématiques et propose un ensemble de fonctions de base : racine carré, puissance, exponentielle, fonctions trigonométriques… Certaines constantes sont également définies, comme \(\pi\).
print("Pi :", np.pi)
print("Racine carrée :", np.sqrt(2))
print("Exponentielle :", np.exp(1))
print("Sinus :", np.sin(3))
L’exemple précédent donne le résultat :
Pi : 3.141592653589793 Racine carrée : 1.4142135623730951 Exponentielle : 2.718281828459045 Sinus : 0.1411200080598672
Problème des listes en Python pour faire des maths
De manière native, Python sait gérer des objets de type list.
a_list = [1,2,3,4,5] b_list = [-1,-2,-3,-4,-5] print(a_list) print(b_list)
L’affichage de ces listes donne le résultat suivant :
[1, 2, 3, 4, 5] [-1, -2, -3, -4, -5]
Ces listes ne sont cependant pas comparables à des vecteurs mathématiques. On peut s’en rendre compte lorsqu’on souhaite utiliser des méthodes de calcul associées à ces objets. En effet, l’addition de deux listes, par l’opérateur +, est en réalité une concaténation de ces deux listes.
print("Addition des deux listes : ", a_list + b_list)
L’affichage obtenu est alors le suivant :
Addition des deux listes : [1, 2, 3, 4, 5, -1, -2, -3, -4, -5]
Impossible alors de faire des sciences avec ce comportement. L’utilisation de la bibliothèque Numpy permet d’ajouter une couche logicielle permettant les calculs vectoriels.
Utilisation de vecteurs
Création d’un vecteur à partir d’une liste
Pour créer un vecteur avec Numpy, il faut utiliser la fonction array.
a_vect = np.array([1,2,3,4,5]) b_vect = np.array([-1,-2,-3,-4,-5])
On peut alors afficher ces vecteurs par l’intermédiaire de la fonction print de Python :
print(a_vect) print(b_vect)
Ces commandes donnent l’affichage suivant :
[1 2 3 4 5] [-1 -2 -3 -4 -5]
Nombre d’éléments d’un vecteur
Pour connaître le nombre d’éléments d’un vecteur, il est possible d’utiliser l’une ou l’autre des commandes suivantes :
print(len(b_vect)) print(b_vect.size)
Création de vecteurs automatiques
Il peut être utile de créer directement un vecteur sans avoir à taper un à un ses éléments, comme nous l’avons fait précédemment.
Plusieurs fonctions de la bibliothèque Numpy permettent de générer automatiquement des vecteurs :
- linspace et arange : pour créer des vecteurs à évolution linéaire entre chaque élément, avec un pas constant
- zeros et ones : pour créer des vecteurs remplis de 0 ou de 1
Vecteurs à évolution linéaire
La fonction linspace permet de générer un vecteur de taille prédéfinie à partir d’une valeur de début jusqu’à une valeur de fin, selon un pas constant dépendant de l’intervalle et de la taille du vecteur.
#np.linspace(début,fin,taille)
x_lin = np.linspace(0,10,15) #Créé un vecteur de taille 15 allant de 0 à 10 à pas constant
print("np.linspace :\n", x_lin)
L’exemple précédent donne le résultat suivant :
np.linspace : [ 0. 0.71428571 1.42857143 2.14285714 2.85714286 3.57142857 4.28571429 5. 5.71428571 6.42857143 7.14285714 7.85714286 8.57142857 9.28571429 10. ]
Il existe également la fonction arange permet de générer un vecteur à partir d’une valeur de début jusqu’à une valeur de fin, selon un pas constant prédéfini.
#np.arange(début,fin,pas)
x_ara = np.arange(0,20,2.1) #Créé un vecteur allant de 0 à 18.9 avec un pas de 2.1
print("np.arange :\n", x_ara)
Cet exemple donne alors le résultat suivant :
np.arange : [ 0. 2.1 4.2 6.3 8.4 10.5 12.6 14.7 16.8 18.9]
Lorsque le pas n’est pas fourni à la fonction arange, cette dernière utilise une valeur par défaut de 1.
Vecteurs pré-remplis de 0 ou de 1
La fonction zeros permet de générer un vecteur de taille prédéfinie dont les termes sont nuls.
#np.zeros(taille) vect_zeros = np.zeros(3) #Créé un vecteur de 3 éléments dont la valeur de chaque élément vaut 0 print(vect_zeros)
De la même manière, la fonction ones permet de générer un vecteur de taille prédéfinie dont les termes valent 1.
#np.ones(taille) vect_ones = np.ones(3) #Créé un vecteur de 3 éléments dont la valeur de chaque élément vaut 1 print(vect_ones)
Opérations sur les vecteurs
Contrairement aux listes natives de Python, les objets de type array sous Numpy permettent le calcul vectoriel.
Addition terme à terme
Par exemple, l’opérateur d’addition + permet de faire une addition terme à terme entre deux vecteurs.
print("Addition des deux vecteurs obtenus à l'aide de numpy : ", a_vect + b_vect)
Cette commande donne le résultat suivant :
Addition des deux vecteurs obtenus à l'aide de numpy : [0 0 0 0 0]
Multiplication des termes par un coefficient
Il est également possible de multiplier tous les éléments d’un vecteur par un coefficient par l’intermédiaire de l’opérateur *.
print("Multiplication d'un vecteur par un nombre (ici 2.1) :", a_vect * 2.1)
La ligne précédente donne le résultat suivant :
Multiplication d'un vecteur par un nombre (ici 2.1) : [ 2.1 4.2 6.3 8.4 10.5]
Multiplication terme à terme
Il est également possible de multiplier des éléments de vecteurs terme à terme par l’intermédiaire de l’opérateur *.
print("Multiplication terme à terme :", a_vect*b_vect)
La ligne précédente donne le résultat suivant :
Multiplication terme à terme : [ -1 -4 -9 -16 -25]
Indexation des vecteurs
L’indexation des vecteurs de Numpy est la même que pour des listes classique en Python.
Dans l’exemple suivant, on génère un vecteur nommé vect_1D de 3 éléments, qui seront indexés de 0 à 2. On accède alors à l’élément i de ce vecteur par la commande vect_1D[i] . Dans cet exemple, on accède au premier élément de ce vecteur.
vect_1D = np.array([1,2,3])
print("Premier élément du vecteur vect_1D :", vect_1D[0])
Concaténation de vecteurs
Il est possible de concaténer des vecteurs entre eux avec par l’intermédiaire de la fonction concatenate.
Dans l’exemple suivant, on génère deux vecteurs x1 et x2 de même dimension que l’on va concaténer l’un à l’autre.
x1 = np.arange(0,5,1)
x2 = np.arange(-2.5,2.5,1)
x_concat = np.concatenate((x1,x2))
print("x1 et x2 concaténés :", x_concat)
On obtient alors le résultat suivant :
x1 et x2 concaténés : [ 0. 1. 2. 3. 4. -2.5 -1.5 -0.5 0.5 1.5]
Comportement avec les fonctions
On peut utiliser les vecteurs dans des fonctions. L’intérêt principal est un gain de temps de calcul par le passage au calcul vectoriel, comparé à l’utilisation de boucles itératives. Le code est également plus lisible.
Méthode classique (non matricielle)
Pour montrer l’intérêt de l’utilisation de vecteurs (ou de matrices par la suite), voici un exemple utilisant des listes classiques. Cet exemple n’est pas à retenir…
#Version avec des listes : à ne pas utiliser !
x_list = [1,2,3,4] #A ne pas utiliser !
for i in x_list: #A ne pas utiliser !
print("exp("+str(i)+") =", np.exp(i)) #A ne pas utiliser !
Cette méthode donne le résultat suivant :
exp(1) = 2.718281828459045 exp(2) = 7.38905609893065 exp(3) = 20.085536923187668 exp(4) = 54.598150033144236
Méthode matricielle/vectorielle
Une solution plus robuste et moins gourmande en temps de calcul est l’utilisation de vecteurs (ou de matrices).
Cette seconde méthode se base sur des vecteurs pour réaliser les même calculs que précédemment :
x_vect = np.array([1,2,3,4])
x_vect_exp = np.exp(x_vect)
print("Avec les arrays de numpy on obtient l'array suivant :", x_vect_exp)
On obtient alors le résultat suivant :
Avec les arrays de numpy on obtient l'array suivant : [ 2.71828183 7.3890561 20.08553692 54.59815003]
Cette méthode est utilisable avec des fonctions que vous avez défini vous même.
Dans l’exemple suivant, on fournit une fonction \(f(x) = 4 \cdot x^2 – 3 \cdot x + 9\) et on souhaite calculer la valeur de cette fonction pour différentes valeurs de x. Ces valeurs sont alors stockées dans un vecteur.
# fonction
def f(x):
return 4*x**2 - 3*x +9
print("Fonction f(x) pour x_vect :", f(x_vect))
On obtient alors l’affichage suivant :
Fonction f(x) pour x_vect : [10 19 36 61]
Affichage graphique des fonctions
Cette méthode vectorielle est utile pour générer les abscisses des graphiques de fonctions mathématiques, que ce soit des vecteurs linéaires ou logarithmiques, et ainsi générer un vecteur de sortie correspondant aux valeurs de la fonction en ces différents points.
Dans l’exemple suivant, on génère un vecteur nommé x de 100 éléments entre les valeurs 0 et 10, qui servira pour calculer ensuite les points d’une fonction \(f(x) = cos(x)\), stockés dans le vecteur nommé y.
from matplotlib import pyplot as plt x = np.linspace(0,10,100) y = np.cos(x)
On pourra par exemple afficher les valeurs stockées dans le vecteur y en fonction des valeurs stockées dans le vecteur x avec la bibliothèque Matplotlib et son module pyplot (voir tutoriel : Premiers pas avec Matlplotlib Pyplot ).
plt.figure(figsize=(15,10))
plt.plot(x,y)
plt.xlabel("x")
plt.ylabel("cos(x)")
plt.title("Tracé de cos(x) entre 0 et 10 avec 100 points")
plt.show()
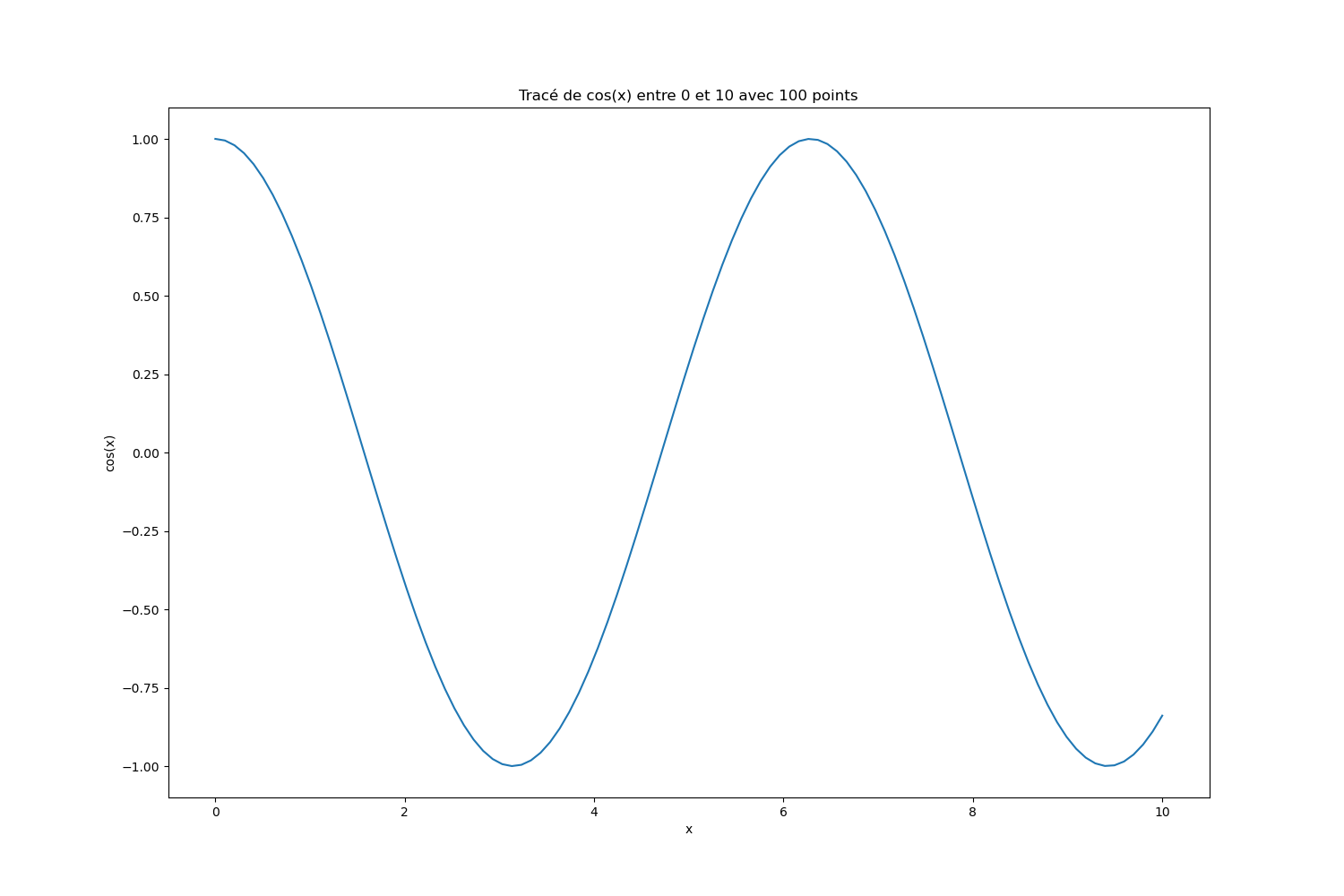
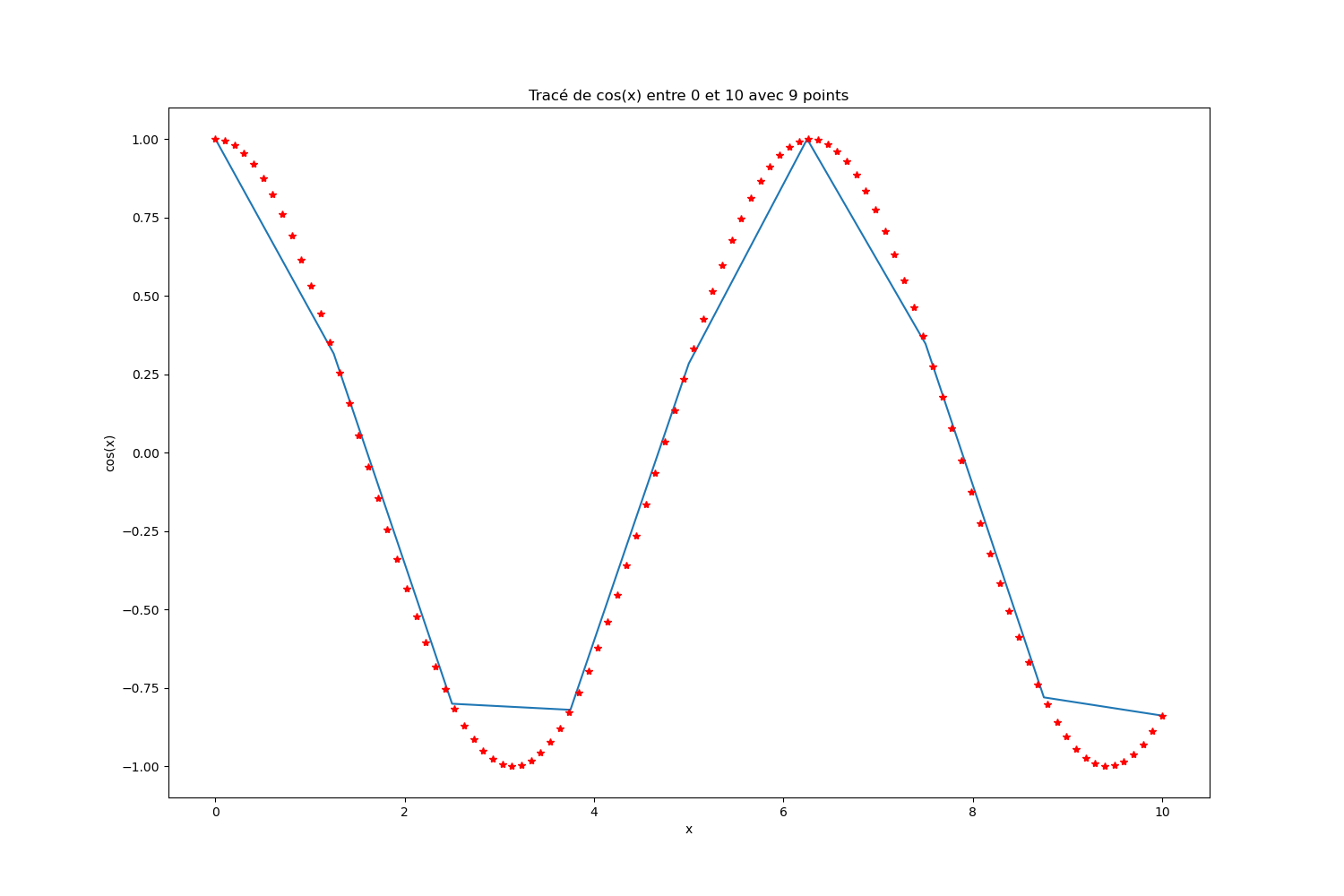
Attention toutefois au pas d’échantillonnage. Dans l’exemple suivant, il n’y a que 9 échantillons sur le même intervalle que précédemment. On remarque que l’affichage de la courbe est moins intéressant.
x = np.linspace(0,10,9) # On met 9 x, le pas est donc plus élevé et la fonction mal échantillonée y = np.cos(x)
Ce tutoriel a été co-écrit par Corentin LE PENDU (promo 2024) dans le cadre d’une semaine spécifique.

