Retour Matlab
Systèmes
Fonction de transfert
Un système peut-être mathématiquement modélisé par sa fonction de transfert \(H(p)\), qui est une fraction rationnelle de deux polynomes \(N(p)\) et \(D(p)\). Il s’agit de la relation qui lie le signal d’entrée au signal de sortie en fonction de la fréquence du signal d’entrée.
Il existe deux moyens sous Matlab pour définir cette fonction de transfert. La première est présentée dans la suite de ce document.
La seconde utilise des boites à outils spécifiques de Matlab et elle est présentée dans le tutoriel suivant : MATLAB / Systèmes et asservissement / Approche système.
Fonction de transfert dépendant de w
La première méthode consiste à utiliser les outils vectoriels de Matlab.
Chacun de ces polynômes dépend de la pulsation \(\omega\) (ou fréquence \(f = \frac{\omega}{2 \pi}\)). Il faut donc créer un vecteur permettant de stocker des valeurs de pulsation :
% vecteur des pulsations, variation log de 10^1 à 10^6 sur 101 points w = logspace(1, 6, 101);
Dans la suite de cet exemple, nous allons nous intéresser à un filtre passe-bas RC, dont la fonction de transfert est : \(H(j\omega) = \frac{1}{1 + j R C \omega}\).
Il est donc nécessaire de saisir les paramètres du modèle, ici R et C :
% paramètres du filtre RC R = 1e4; C = 1e-7;
On peut à présent définir les deux polynomes : numérateur (\(num\)) et dénominateur (\(den\)) ainsi que la fonction de transfert (\(TF\)) :
% fonction de transfert num = 1; den = 1 + j * R * C * w; TF = num ./ den;
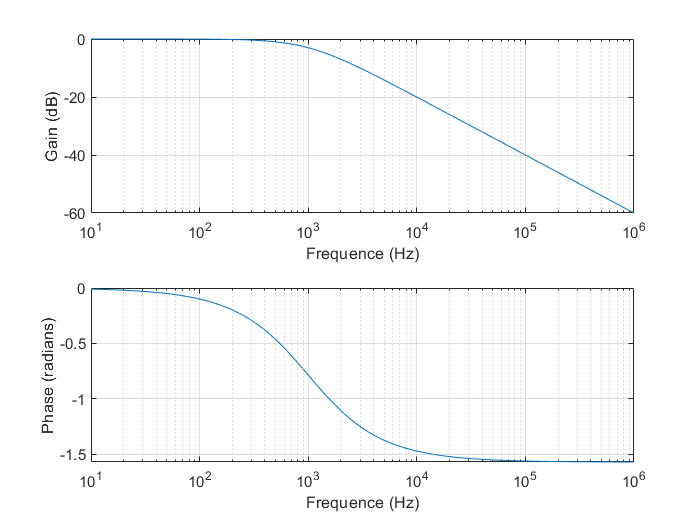
Diagramme de Bode d’un système
A partir de la fonction de transfert calculée précédemment, il est possible de calculer alors le gain en dB et la phase de cette fonction de transfert de la manière suivante :
% calcul du gain et de la phase gain = 20*log10(abs(TF)); phase = angle(TF);
On peut alors tracer le diagramme de Bode dans deux sous-figures de la manière suivante :
subplot(2,1,1);
semilogx(w,gain);
xlabel('Frequence (Hz)');
ylabel('Gain (dB)');
grid on;
subplot(2,1,2);
semilogx(w,phase);
xlabel('Frequence (Hz)');
ylabel('Phase (radians)');
grid on;
On obtient alors une courbe de la forme suivante :