Sommaire
Comment faire varier la vitesse d’un moteur à courant continu ?
NIVEAU 3
Objectifs
- Comprendre le fonctionnement d’un moteur à courant continu
- Piloter un moteur à courant continu à l’aide d’un microcontroleur
Pré-requis
Moteur à courant continu
Un moteur à courant continu est un système permettant de transformer une énergie électrique en mouvement de rotation continue. Ce type de moteur doit être parcouru par un courant continu.
Il est contitué :
- d’un inducteur (souvent le stator, fixe)
- d’un induit (souvent le rotor, mobile)
- de balais et de collecteurs
La figure ci-dessous (image de Energie+) montre le principe de création d’une force électromagnétique à partir de l’inducteur dans l’induit traversé par un courant :
D’après la loi de Laplace (tout conducteur parcouru par un courant et placé dans un champ magnétique est soumis à une force), les conducteurs de l’induit placés de part et d’autre de l’axe des balais (ligne neutre) sont soumis à des forces F égales mais de sens opposé en créant un couple moteur : l’induit se met à tourner !
Modèle du moteur à courant continu
On peut modéliser un moteur à courant continu de cette façon là :
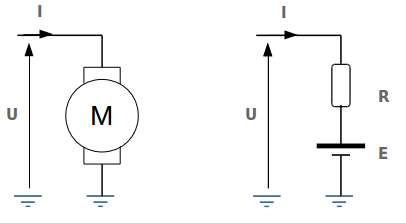
Transformation de puissance
La puissance électromagnétique \(P_{em}\) mise en jeu dans un moteur à courant continu peut s’exprimer de deux façons différentes :
- Aspect électrique : \(P_{em} = E \cdot I\)
- Aspect mécanique : \(P_{em} = T_{em} \cdot \Omega\)
où :
- \(E\) : la force contre-électromotrice [volt]
- \(I\) : le courant dans l’induit [ampère]
- \(T_{em}\) : le couple du moteur [N.m]
- \(\Omega\) : vitesse angulaire de l’induit [rad/s]
Relation entre la tension et la vitesse de rotation
Lorsque l’induit est alimenté sous une tension continue, nommée \(U\), il se produit une force contre-électromotrice notée \(E\).
On a alors la relation suivante : \(E = U – R \cdot I\)
où :
- \(R\) : la résistance de l’induit [ohm].
- \(I\) : le courant dans l’induit [ampère]
- \(E\) : la force contre-électromotrice [volt]
- \(U\) : la tension aux bornes du moteur [volt]
La force contre-électromotrice \(E\) est liée à la vitesse \(\Omega\) et à l’excitation du moteur \(\Phi\) par la relation suivante :
\(E = k \cdot \Phi \cdot \Omega\) où :
- \(k\) : constante propre au moteur (dépendant du nombre de conducteurs de l’induit)
- \(\Phi\) : flux de l’inducteur [weber]
- \(\Omega\) : vitesse angulaire de l’induit [rad/s]
En analysant la relation ci-dessus, on voit que la force contre-électromotrice \(E\) est proportionnelle à la vitesse de rotation (à excitation constante de l’inducteur). On peut aussi noter que si la tension devient négative, la vitesse de rotation est inversée aussi.
Relation entre le courant et le couple du moteur
Quant au couple moteur, il est lié au flux inducteur et au courant de l’induit par la relation suivante : \(T_{em} = k \cdot \Phi \cdot I\)
où :
- \(k\) : constante propre au moteur (dépendant du nombre de conducteurs de l’induit)
- \(\Phi\) : flux de l’inducteur [weber]
- \(I\) : courant dans l’induit [A]
- \(T_{em}\) : couple du moteur [N.m]
Modélisation dynamique
Il existe un modèle plus complet d’une machine à courant continu qui fait apparaître une inductance (côté schéma électrique). Côté mécanique, on peut également appliquer le principe fondamental de la dynamique en rotation autour de l’arbre du
moteur. Il en vient les équation suivantes, en isolant le rotor :
- En absence de frottement : \(T_{em}(t) = J \cdot \frac{d\Omega(t)}{dt}\)
- Avec frottement et couple résistant : \(T_{em}(t) – T_r(t) – f \cdot \Omega(t) = J \cdot \frac{d\Omega(t)}{dt}\)
où
- \(J\) : moment d’inertie du rotor
- \(f\) : coefficient de frottements fluides
- \(C_r\) : couple résistant au moteur
Après simplification, on obtient le modèle suivant pour la fonction de transfert entre la vitesse de rotation (en sortie du moteur) et la tension appliquée (en entrée) : \(H_m(p) = \frac{\Omega(p)}{U(p)} = \frac{K_0}{(1 + \tau_m \cdot p)(1 + \tau_e \cdot p)}\)
où
- \(\tau_m = \frac{R \cdot J}{k^2 + R \cdot f}\) : constante mécanique
- \(\tau_e = \frac{L}{R}\) : constante électrique
- \(K_0 = \frac{l}{k^2 + R \cdot f}\) : conversion électromécanique
Commande d’un moteur à courant continu
Constantes de temps
Dans le paragraphe précédent, on a vu que la modélisation complète (simplifiée) d’un moteur à courant continu (fonction de transfert entre vitesse de rotation et tension d’entrée) donnait une équation du second ordre possédant 2 constantes de temps distinctes.
En mesurant ces différentes constantes de temps, on s’aperçoit que la constante de temps électrique est souvent très faible (i.e. un système passe-bas avec une bande-passante élevée). Au contraire, la constante mécanique est plus grande (due à l’inertie souvent importante des rotors – en particulier sur les moteurs de forte puissance).
On parle souvent d’une constante de conversion électro-mécanique “lente”. Ainsi, en appliquant un signal électrique de commande “rapide”, type PWM, le mouvement mécanique associée n’en verra que la valeur moyenne.

Commande par modulation de largeur d’impulsions / MLI – PWM
En utilisant le principe de la modulation de largeur d’impulsions (MLI ou PWM – voir tutoriel Régler la luminosité d’une LED) et en appliquant le signal résultant sur un moteur à courant continu, on va pouvoir contrôler la vitesse de rotation de ce dernier.
Exemple simple
#include "mbed.h"
PwmOut moteur_cc(D10);
int main() {
double rc = 0.2;
moteur_cc.period_ms(10);
moteur_cc.write(rc);
while(1);
}
Adaptation en puissance
La plupart des moteurs à courant continu ne sont pas compatibles avec les courants délivrables par les microcontroleurs. Il faut passer par des étages d’adaptation de la puissance, en particulier en utilisant des transistors.
Dans le cas d’une commande dans un seul sens de rotation, on peut utiliser un seul transistor de puissance comme dans le montage suivant :
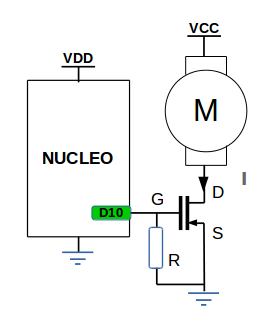
Sur ce montage, lorsque la sortie D10 est à ‘0’, le transistor n’est pas commandé, il se comporte alors comme un circuit ouvert entre les broches nommées D et S. Il n’y a pas de courant qui passe dans la branche du moteur. Il ne tourne donc pas.
Lorsque la sortie D10 est à ‘1’, le transistor est commandé, il se comporte alors comme un circuit fermé entre les broches nommées D et S. Il y a passage de courant dans la branche du moteur. Il peut tourner !
La résistance \(R\) est une résistance d’une dizaine de kiloohms, permettant d’assurer le passage d’un courant minimal sur la sortie D10.
Commande réversible en sens de rotation
Pour pouvoir piloter un moteur à courant continu dans les deux directions, il faut pouvoir inverser le sens du courant (et de la tension aux bornes du moteur).
Pour cela, on peut s’intéresser à des structures qui permettent cette inversion : des ponts en H. Il s’agit de la mise en série et en parallèle de 4 transistors du même type :
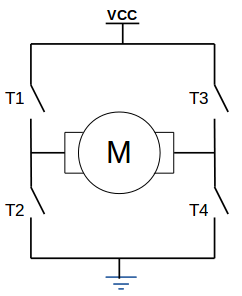
Selon la commande appliquée aux différents transistors, on peut appliquer une tension dans un sens ou dans un autre sur le moteur. Pour cela, il faut piloter deux à deux les transistors :
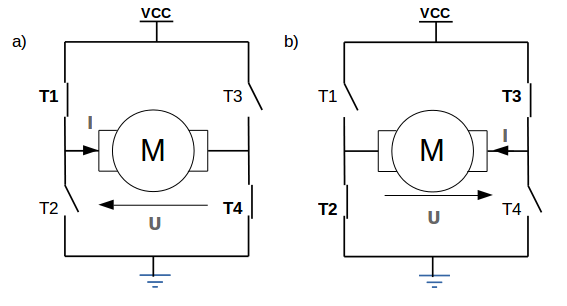
Dans le cas a), les transistors T1 et T4 sont commandés. Ainsi la tension et le courant sont positifs dans le sens indiqué.
Dans le cas b), les transistors T2 et T3 sont commandés. Ainsi la tension et le courant sont positifs dans le sens opposé au précédent cas.
En appliquant successivement un signal PWM sur les couples T1/T4 et T2/T3, on peut alors faire tourner le moteur à courant continu dans un sens ou dans un autre à une vitesse proportionnelle au rapport cyclique du signal appliqué.
Pont en H intégré
Il existe des composants intégrant des ponts en H complet. On peut citer par exemple le L293D (800mA environ sous 30 V) ou le L298 (2A sous 30V).
Exemple de code
#include "mbed.h"
PwmOut moteur_cc1(D10);
PwmOut moteur_cc2(D9);
DigitalIn bouton(USER_BUTTON);
int main() {
double rc;
char c;
moteur_cc1.period_ms(10);
moteur_cc2.period_ms(10);
moteur_cc1.write(0);
moteur_cc2.write(0);
while(1){
if(bouton == 1){
moteur_cc2.write(0);
moteur_cc1.write(rc);
}
else{
moteur_cc1.write(0);
moteur_cc2.write(rc);
}
}
}
Dans le code proposé, l’utilisateur doit à présent saisir la direction (A pour anti-horaire, H pour horaire) ainsi que le rapport cyclique souhaité. On utilise alors 2 sorties PWM : une pour piloter les transistors T1 et T4 en même temps, et l’autre pour piloter les transistors T2 et T3 en même temps.
N.B. Il existe des composants tout intégrés permettant de réaliser des ponts en H : par exemple, le L293D.
Matériels
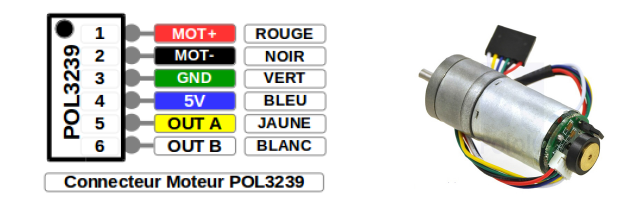
MCC Pololu 3239
Il s’agit du moteur Pololu POL3239
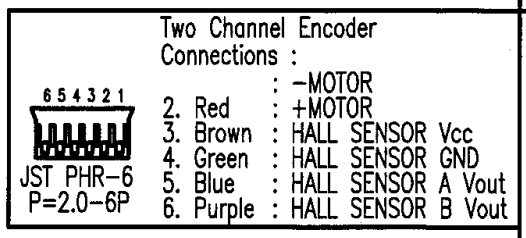
MCC Digilent
Il s’agit du moteur de référence 134-6440 chez Radiospares.
Moteur Brushless
A VENIR
MInE Prototyper Prototyper avec Nucleo et MBED

